Quick links
- Randomized depth-first search
- Bloxorz
- Functional Program Design in Scala
- Gist for fable.io/repl
- fable.io/repl
- Online demo
- Gist with bits and bobs
Rant (just a little one)
First book I ever read on computer science was “Algorithms + Data Structures = Programming“ by Niklaus Wirth. For a very long time, my favorite one was “Introduction To Algorithms“ by Thomas Cormen. You can see the pattern, right?
It the era of JSON-over-HTTP neither algorithms nor data structures and considered necessary for programming. Actually, it is considered a success if someone choses the right data structure, not mentioning implementing it or, at least, understanding how it works. It is kind of understandable as it is no longer required to understand B+ Trees to use SQL database.
But it helps. And it is fun.
BFS
Breadth-First Search is tree traversal algorithm. Because tree is a graph without cycles, by just tracking visited nodes (and preventing cycles) we can use it to build spanning tree of any graph.
I touched the topic of spanning trees quite some time ago while writing about maze generation (which can be implemented as “random spanning tree”).
Breadth-First Search can be expressed with three steps:
- take first node from the queue, mark it as visited and return it
- append all unvisited child nodes to the end of the queue
- rinse and repeat
1 | let bfs idof fanout node = |
This is neither the most generic implementation of BFS nor the (functionally) purest. For example, both Queue and HashSet are mutable data structures and it uses while loop instead of recurrence, but in this case it is probably most pragmatic one. There is no problem with imperative code in F# (multi-paradigm, functioanl first) as long as it is properly encapsulated. You can read more about this on Eirik Tsarpalis’ blog.
You can see I’m a fan of micro DSLs which allow me express “the essence” without any technical noise. It makes implementation a little bit longer sometimes, but in my opinion, much more readable. There are multiple ways to make this implementation slighlty bit shorter (first step would be using tap/tee function in few places), but they don’t improve readability so I’ll leave it as it is.
Let’s talk about this function then.
The types are properly inferred by F# compiler and there is no need to declare them explicitly but in this case it would be actually beneficial to do it (adding explicit type declaration on public interfaces is generally a good idea):
1 | let bfs (idof: 'node -> 'id) (fanout: 'node -> 'node seq) (node: 'node) = //... |
So:
idof: 'node -> 'id: a function which will take the node and generate something which can be considered node’s id; if node is its own id it would be sufficient to use built-inidfunction (which isfun x -> x); please note, that it is actually ids which are stored inHashSetand used to determine visited nodes;fanout: 'node -> 'node seq(to be more precise'node -> 'nodes when 'nodes :> seq<'node>): a function which will take a single node and return all adjacent nodes (in tree they would be just child nodes)node: 'node: a starting node
Let’s test it with some simple tree defined as Map<int, int list>.
I would use example from wikipedia:
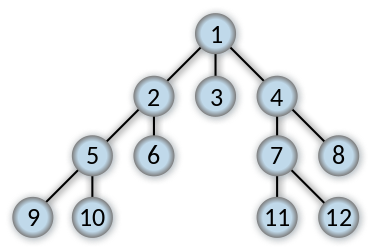
1 | let tree = |
Map.find (which is int -> int list) matches almost exactly signature required by fanout ('node -> 'node seq) but let’s make it a little bit more resilient by using Map.tryFind:
1 | let fanout node = tree |> Map.tryFind node |> Option.defaultValue [] |
It will try to find node in tree and return list of its children. If no children are found it will return empty list ([]).
Now we can call it:
1 | bfs id fanout 1 |> List.ofSeq |
and… (drum roll):
1 | [1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12] |
Yay! Exactly as expented. You can add cycles (for example: 2, [5, 6, 1]) to test if cycles are properly eliminated.
NOTE: To run it in fable.io/repl you will need to polyfill Queue, for example:
1 | type Queue<'a>(values: 'a seq) = |
Scanning directories with BFS
One of the examples of tree traversal algorithms is listing directories. I never really cared which tree traversal algorithm, DFS or BFS, is used for that. I was actually suprised that Unix find works differently than PowerShell gci (Get-ChildItem). Apparently, find uses DFS while gci uses BFS.
1 | find -type d | less |
1 | gci -r -dir | % { $_.FullName } | oh -p |
Let’s assume I want to do something like Get-ChildItem (or like find, but with BFS). How can I implement this using bfs method?
First question is: what is the node? The node in this case is directory. Directory access in .NET can be done with DirectoryInfo class from System.IO namespace. What is fanout function? This function will take take a directory and return list of child directories. Last thing left is idof function returning something which can be used to uniquely identify directory. Let’s say full directory name is good enough in this case (although, something like “inode” or “files system object id” would be much better, as it would resolve potential sym-link cycles).
So, having idof, fanout and node defined as follows:
1 | open System.IO |
we can run it with:
1 | bfs idof fanout node |> Seq.toList |
…and get list of all child directories.
Let’s refactor this into a function:
1 | let scanFolders path = // string -> string seq |
which takes path as input and returns sequence of folder names (scanFolders: string -> string seq).
We can run it with, for example:
1 | scanFolders "." |> Seq.iter (printfn "%s") |
Please note, that this time we really needed to use idof as DirectoryInfo is an object without structural equality so DirectoryInfo(".") != DirectoryInfo("."). To compare them we needed something else, something comparable and DirectoryInfo.FullName look like a good-enough choice.
It would be actually safer to use slightly modified version of fanout to suppress exceptions in directories which we have no access to:
1 | let fanout (node: DirectoryInfo) = |
Tracing the path
Sometimes, apart from getting there (visiting nodes) it is important to know “how we got there” (keeping a history of decisions). We do not want to rewrite bfs, we would like to reuse it. Let’s call this new method trace. So far, bfs is taking node ('node) and fanout function (fanout: 'node -> 'node seq) and returns a sequence of nodes ('node seq).
This paragraph, describing transformation from bfs into trace is probably the most convoluted one in this post. I tried to rewrite it many times but I couldn’t make it simpler (my fault). It is very important though, so please read multiple times until you think you understand what happens here.
We want trace to return not only a sequence of nodes ('node seq) as bfs does but also a history of actions which led to this node: ('node * 'action list) seq. Look again, instead of sequence of 'node we want a sequence of 'node * 'action list. We don’t know nor care what 'action is. We want it to be provided from fanout. The new fanout will not only return a sequence of child nodes ('node -> 'node seq) but also an action which caused this transition. New fanout will be 'node -> ('node * 'action) seq - taking node and returning sequence of child nodes and actions leading to them. We will reuse bfs by providing little adapter functions for idof, fanout and node.
Both new node and new idof are relatively simple. New starting node is a node with empty action history while new idof will just ignore action history (as how we got to given node does not affect node’s identity):
1 | let node' = (node, []) |
Adapter for fanout is a little bit more complicated. The node passed to bfs is no longer just node, but also contains action history ('node * 'action list) so fanout expected by bfs should be 'node * 'action list -> ('node * 'action list) seq, but it isn’t. Our new fanout (for trace) is (as mentioned before) 'node -> ('node * 'action) seq. So, we will need another adapter:
1 | let fanout' (node, actions) = node |> fanout |> Seq.map (fun (n, a) -> (n, a :: actions)) |
Now, types match again: fanout is 'node -> ('node * 'action) seq while fanout' is 'node * 'action list -> ('node * 'action list) seq.
Let me try to explain one more time: fanout' will take a pair of node and actions (leading to this node), it will use fanout with node (action history is irrelevant at this point) returning sequence of nodes and actions (n, a) and create new states with those new nodes and new action prepended to history (fun (n, a) -> (n, a :: actions)).
So, whole trace function is:
1 | let trace idof fanout node = |
Please note that new actions are prepended to action list (a :: actions) so actions will be returned in reversed order. It is not a problem, it is just worth remembering.
Let’s run it using the tree we used before.
1 | let tree = |
The only question is what we want the action to be in this case? There is no left or right, as the only decision is down. Let’s use source node as action, so the history of actions will be actually history of nodes.
1 | let fanout node = |
We can run it now:
1 | trace id fanout 1 |> List.ofSeq |
and get the all the nodes with traversal history:
1 | [ |
We can of course process it further, prepending final node to history and then reversing order:
1 | trace id fanout 1 |> Seq.map (List.Cons >> List.rev) |> List.ofSeq |
to transform it to paths:
1 | [ |
This is still not finished thought: trace calls bfs while actually it does not care if underlying algorithm is BFS. It would work absolutely perfectly with any other algorithm (DFS, for example). Let’s extract it then:
1 | let trace traverse idof fanout node = |
As you can see, trace does not call bfs directly anymore, it expects function of matching signature to be passed to it. bfs is a perfect candidate, and works perfectly:
1 | trace bfs id fanout 1 |> List.ofSeq |
But now, we could use it with (hypothetical) dfs by just changing it to:
1 | trace dfs id fanout 1 |> List.ofSeq // NOTE: you would have to implement dfs yourself |
Please note, that with one trivial adapter function (idof'), one relatively simple adapter function (fanout') and injectable traversal algorithm (bfs, dfs or… whatever matches the signature) we have completely new functionality (tracing). Composite Reuse Principle, Single Responsibility Principle, Open/Closed Principle, Interface Segregation Principle and Dependency Inversion Principle. All of those in 5 lines of code.
Bloxorz
The idea of doing Bloxorz solver comes from Functional Program Design in Scala course. It is a second week assignment. In does not explicitly mentions BFS as it tries to teach lazy evaluations rather than graph algorithms, but I find a great example how to use BFS.
Unfortunately, it is quite hard to explain how it works, so you will need to play Bloxorz yourself on, for example: http://www.bloxorz.org.uk/ (you will also need to enable Flash). If it doesn’t work just google “bloxorz” and you may find multiple sites allowing you to play. If it is year 2050, Flash no longer works, and nobody ported Bloxorz to ES2050, but YouTube still works you can check what it was about here:
If you have a feel how Bloxorz work we can start. We will address only the simplest scenarios: no weak squares, no block splitting and no dynamic environment. While weak squares could be actually quite easy to implement, block splitting and dynamic environment would bring a lot of complexity to solution.
As I already hinted we will use BFS to solve Bloxorz puzzles. Knowning that we need to establish what node will be, what idof should return and how fanout should work.
The node is the state/position of the block. The child/adjacent nodes are the valid nodes which can be reached by moving block in any direction. Valid node is the node where both parts of the block are on valid squares. The solution is the path (history of actions) leading to target block position while target block position is block “standing” on top of the goal. Yeah, that’s why you need to play Bloxorz for a while to get a feeling what all those things mean.
Let’s start with a little bit of domain:
1 | type Position = int * int |
For functional purists: I have to admit that this domain model violates make illegal state unrepresentable principle. For example, we can define split Bloxor while we said we are not handling them. We can also construct a World when one or both (starting and target) positions are illegal. Although, I decided that domain design for Bloxor problem is not really a main topic here.
So, we have Position which represents X and Y coordinates in Bloxor space. We have Bloxor which is a pair of positions (as it consists of two pieces). We have World which has starting position (A), target position (B) and a function answering the question: is given position legal (takes Position and returns true or false).
Let’s define infinite World first:
1 | let infiniteWorld a b = { A = a; B = b; IsValid = fun _ -> true } |
Please note that IsValid always returns true, which means any position is legal, we can roll our bloxor wherever we want. We will implement more complex worlds later but this one will allow us to have something to test our algorithm with.
Let’s define some functions around bloxor behaviour and state. First, makeBloxor will allow us to create a standing bloxor at given position. This is a lot of text to create tuple of points (p, p) but let’s make it official:
1 | let makeBloxor (position: Position): Bloxor = (position, position) |
The other helper function would help us determine what is current bloxor orientation:
1 | let (|IsStanding|IsHorizontal|IsVertical|) (bloxor: Bloxor) = |
I assume you are familiar with active patterns, but even if you are not, please imagine three methods (IsStanding, IsHorizontal and IsVertical) so similar that thay share single body… Well, it does not make it any clearer. I guess “Multi-Case Active Patterns” section on Chris Smith’s blog explains it better.
This active patterns deconstructs bloxor and recognizes its orientation: standing, horizontal or vertical. It may also throw an exception when bloxor is invalid (including split or just inverted). It requires some discipline how bloxor is constructed but as I said before, MISU principle is not a main concern here.
Next step is to define how bloxor moves. This is really messy function (all those shiftY -2 -1 and shiftX -1 -1) but describes all possible moves (North, South, East, West) from all posible startings orientations (IsStanding, IsHorizontal, IsVertical). It decides how bloxor coordinates should be adjusted (let move = match bloxor, direction with ...) and returns new bloxor position (move bloxor).
1 | let moveBloxor (bloxor: Bloxor) (direction: Move): Bloxor = |
The rules were slowly reconstructed from this picture:
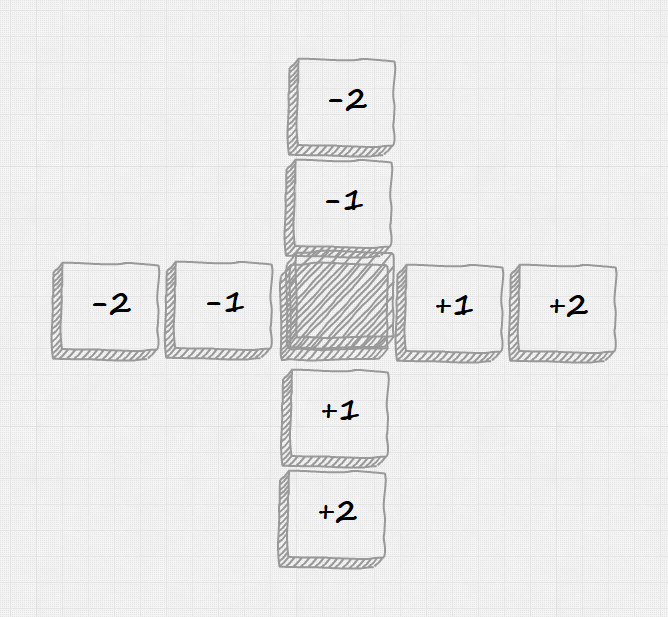
We are ready to write solver function. The solveWorld function will take World (as World is the problem to solve) and return Move list option. We could alias Move list as Path and then returned type would be Path option. It returns option as it possible that solution cannot be found.
1 | let solveWorld (world: World): Move list option = // ... |
Let’s go slowly through DSL for this function:
1 | let solveWorld (world: World): Move list option = |
isValid: bloxor position (deconstructed intoaandb) is valid when both pieces are valid;isFinal: bloxor position (deconstructed intoaandb) is final when both pieces are in final position (meaning: we found the solution);validMoves: try to move bloxor in all directions ([North; South; East; West] |> Seq.map moveBloxor) creating pairs of new bloxor positions and move directions (note:nodeandaction) but filter out all invalid moves (Seq.filter isValid);
We are ready now solve bloxorz! The whole function is:
1 | let solveWorld (world: World): Move list option = |
Where:
node: bloxor initial position atworld.A;idof: bloxor position unique identifier - it is just a string with coordinates of both pieces; because of structural equality in F# this is not really needed (built inidwould be sufficient) but it wouldn’t work in Fable (HashSetis not fully compatible);fanout: it is actuallyvalidMoves- for every bloxor position returns a sequence of new valid bloxor positions with appropriate moves (Bloxor -> (Bloxor * Move) seq) which is exactly when we wanted fortrace('node -> ('node * 'action) seq).
So, the last expression is actually running it (trace bfs idof fanout node) which returns a sequence of all paths, and finding first one (shortest!) leading to solutions (Seq.tryFind/isFinal) and taking only the history part (fun (_, actions) -> actions) and reverses it (List.rev). If you’re fan of point-free style, this can be also expressed as:
1 | trace bfs idof fanout node |> Seq.tryFind (fst >> isFinal) |> Option.map (snd >> List.rev) |
Let’s try it first with inifinite world:
1 | infiniteWorld (0, 0) (1, 0) |> solveWorld |
produces:
1 | Some [North; East; South] |
which is the correct answer: solution was found (Some) and the path was North, East, South.
Let’s try a longer path, for example from (0, 0) to (9, 9). We expect it be 6 times South then 6 times East (or the other way around: 6 times East then 6 times South).
1 | infiniteWorld (0, 0) (9, 9) |> solveWorld |
returns:
1 | Some [South; South; South; South; South; South; East; East; East; East; East; East] |
which confirms our expectations.
As a last step, we can add ability to define more complex worlds. Let’s assume we would like to define world using ASCII, for example:
1 | let world = [ |
would represent:

Note, space represents empty sqaure while A and B are initial position and target position respectively.
We need to create a map of characters (Map<int * int, char>) first:
1 | let map = |
This does not look too attractive as, in general, nested loops with indexes are not the prettiest constuct in functional languges. The general idea here is to iterate over lines (world |> Seq.mapi) then over characters in line (l |> Seq.mapi), flatten nested list (Seq.collect) and create a map (x, y) -> c (Map.ofSeq).
Having such a map we can determine initial and target positions:
1 | let a = map |> Map.findKey (fun k c -> c = 'A') |
and define a function which will test if given position is valid:
1 | let valid k = map |> Map.tryFind k |> Option.filter (fun c -> c <> ' ') |> Option.isSome |
Having these three bits of information we can construct a World record:
1 | { A = a; B = b; IsValid = valid } |
Let’s put all those things together:
1 | let parseWorld lines = |
For OO fans I would like to emphasize, that you can think about infiniteWorld and parseWorld as two constructors of two different objects implementing the same interface (World).
So, let’s try this example:
1 | let world = [ |
It returns:
1 | Some [ |
I can bet that’s exactly what we need (you can go to http://www.bloxorz.org.uk/ and use 918660 as stage code).
I wrote simple Fable app which shows results as animation:
- check it here
- or go to gist and paste it into fable.io/repl (you will be able to play with sources a little bit)
…but where FFS is John McClane?
…you might ask. Good question. You need to watch this first (ok, YouTube keeps removing this clip, so if it is gone, try this link):
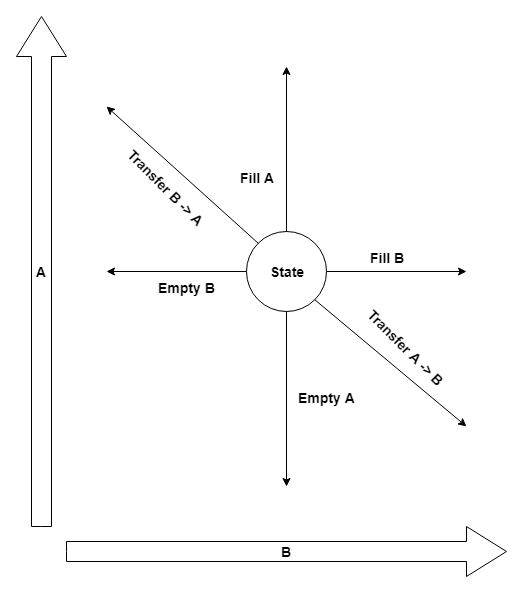
We have solution space (two containers), we have allowed moves (fill, empty, transfer) and a goal (one container contains exactly 4 gallons). Well, this problem is identical to Bloxorz, isn’t it?
Let’s start with domain:
1 | type Jug = | A | B |
Jug: we have two jugs:AandB;Action: possible actions are emptying a jug (Empty), filling a jug (Fill), or transferring water from one jug to another (Transfer);State: state of the system with current and maximum levels;
Let me try to draw it:
We can add some methods to State to make working with this record a little bit easier:
1 | type State = |
Where:
Get: gets jug level;Max: gets jug capacity;Empty: empties given jug;Fill: fills given jug;Transfer: transfers water from one jug to another (until source jug is empty or target jug is full);
These three last methods (Empty, Fill and Transfer) map directly to Action cases:
1 | let applyAction (state: State) action = |
Having all this we can attempt to save New York, and in principle, it is the same operation as solving Bloxorz:
1 | let saveNewYork target state = |
We can identify visited states with idof to avoid running in circles, we can transition to new states with fanout by executing all the possible actions ([Empty A; Empty B; Fill A; Fill B; Transfer (A, B); Transfer (B, A)]), and we can check if we reached our goal (isDone). The last step is actually to scan solution space (trace bfs idof fanout state), terminating search when appropriate (Seq.tryFind) and reversing action history (as it is upside-down).
Let’s try:
1 | let newYork = State.Create(3, 5) |
which returns:
1 | Some [Fill B; Transfer (B,A); Empty A; Transfer (B,A); Fill B; Transfer (B,A)] |
Hmm, let’s replay all actions to see if it really worked. To do that I will actually use some dreaded imperative code:
1 | let newYork = State.Create(3, 5) |
which generates readable description what has happened:
1 | 0/0 -> Fill B -> 0/5 |
and, yes, in fact we end up with 4 gallons in jug B. New York is saved!
Please note, functional purists might say I should not use imperative loop with mutable variable, and use Seq.scan |> Seq.iter instead. To be honest, I did that at first, but this imperative loop is actually much more readable even if not pure enough.
Let’s try something bigger:
1 | State.Create(113, 97) |> saveNewYork 66 |
returns:
1 | Some [ |
Let’s see it it crashes, or hangs up when there is no solution:
1 | State.Create(12, 6) |> saveNewYork 4 |
Nope, it works just fine and returns None.
Conclusion
I really like the idea that three seemingly different problems (scanning folders, pushing Bloxorz through the hole and saving New York) are actually the same problem, and all of them can be solved with the same function and a little bit of “adaptation”.
I also really liked the idea that it is possible to present 4 (out of 5) SOLID principles (plus CRP) in 5 lines of code and the fact that they come quite naturally in FP. Oh irony! OO principles are intrinsic to FP.
Other than that? Well… I don’t think my day-to-day JSON-over-HTTP activities require a lot of “Saving New York”, but when they do, I’m ready :-)