Curious case of disjoint-set

While implementing Kruskal’s algorithm to build mazes (also known as random spanning trees) I encountered interesting problem. Randomized version of Kruskal’s algorithms is quite simple: take any edge, if it would form a cycle reject it (as it will not be a tree anymore) otherwise accept it. That’s it. It’s really simple, there is only one problem: how to detect cycles.

On this picture you can see two separate trees (a forest):

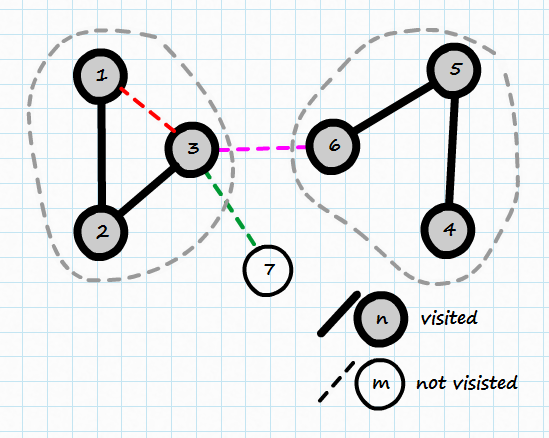
Forest

It is quite clear that connecting 3 and 7 won’t form a cycle as vertex 7 has not been visited yet. The difference between edges 3-1 and 3-6 is not so obvious anymore. All of those vertices (nodes) are visited, but 3-1 will form a cycle, while 3-6 will not.

It would help if we knew which tree given node belongs to, as cycle is formed only when connecting two visited nodes from the same tree (3-1). When connecting visited nodes from different trees, we do not create a cycle, we just connect two trees forming new bigger tree (3-6).

Storing something like TreeId on each node and updating it when trees are merged would theoretically work but would be quite slow. Imagine that we just added single edge connecting two trees, let’s call them A and B. What we would need to do now is to update all nodes from smaller tree (let’s say it is B) and tell them “you are tree A now”. Now let’s assume both trees have 1000000 vertices… oops.

We need a better data structure to store such sets and, fortunately, there is one. It is called disjoint-set (also known as union-find or merge-find set) and it serves exactly that purpose.

How it works?

Disjoint-set organizes items into trees where every item has a parent. Two items belong to the same set when they have same parent.
Let’s start with set of items where no merges has been done so every item is in its own separate set:

Seven distinct sets

Merge

Merging two items into set is about assigning one as a parent of the other one:

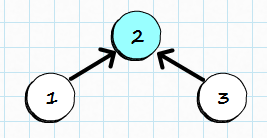
One set with 3 items

Now, the root 2 identifies the whole set so the question “Which set item 1 belongs to?” is answered by “It belongs to set 2“. You can also say: 2 is representative items for the whole set.

On the diagram below, we can see two sets: set 2 and set 5. Items 1, 2 and 3 belong to set 2, while items 4, 5, 6, 7 belong to set 5. Which items becomes a root in merging process is irrelevant although we will try to limit the height of the tree to reduce potential number of hops.

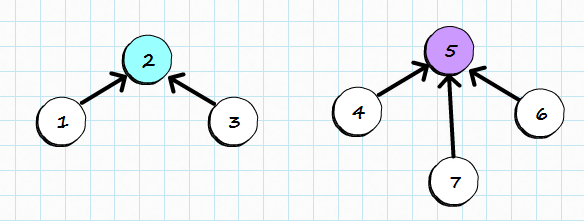
Two sets, one with 3 the other with 4 items

Merging sets works exactly as it was shown before but it will be clearer with the picture:

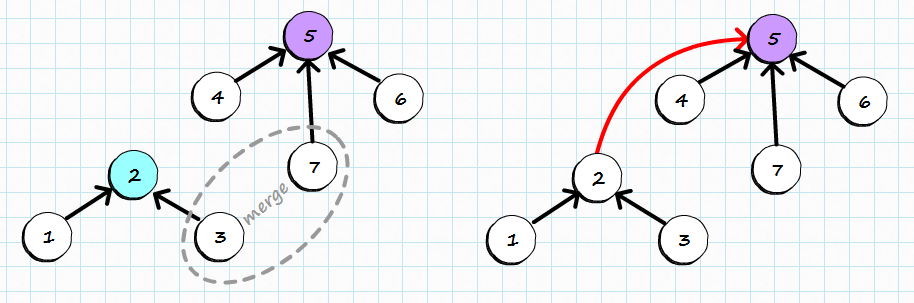
Merging sets

We are trying to merge set containing item 3 with set containing item 7. First we need to find roots of those items (2 and 5 respectively) and then make one the parent of the other one. For algorithm correctness it can be either of those roots, but for performance reasons we choose the root of the higher one as new root. It helps keeping the tree relatively flat, as attaching tree of height 2 to the root of tree of height 3 does not change overall height. If both trees are of equal height we choose one arbitrarily and increase the height of resulting tree. That’s exactly what happened on the picture above, when two trees of height 1 (single item is height 0) formed new tree of height 2 after being merged.

With little though experiment, we can show that minimal tree of height 0 is a single item and minimal tree of height 1 is two items. As height increases only when merging trees of the same height tree of height 2 has to have at least 4 item. Merging two trees of height 2 creates tree of height 3 with at least 8 items. I guess, you can spot the pattern: there is minimum of 2^h items in the tree of height h, therefore finding a root has a pessimistic complexity of O(logn). I emphasized the word pessimistic as usually it does much better.

Find with path compression

Finding a root of element can be used to compress the path at same time. As item’s potentially distant root is found, its parent can be updated to point directly to this root therefore compressing the path.

While merging 3 and 8 on the picture below:

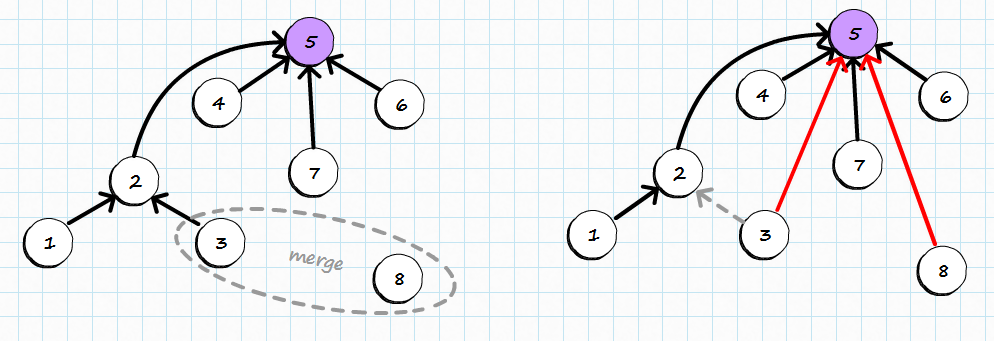
Merging sets with compression

two things can be spotted:

  • root of 3 has been found (5) and parent information has been updates so 3 points to 5 directly from now on
  • 8 is a smaller tree than 5, so 5 becomes a parent of 8

Because of these two techniques union by rank and path compression amortized complexity is lower than O(logn). Wikipedia says:

These two techniques complement each other; applied together, the amortized time per operation is only O(a(n)), where a(n) is the inverse of the function n = f(x) = A(x,x), and A is the extremely fast-growing Ackermann function. Since a(n) is the inverse of this function, a(n) is less than 5 for all remotely practical values of n. Thus, the amortized running time per operation is effectively a small constant.

I actually love the “is less than 5 for all remotely practical values of n” part.

Implementation

All items in set need two properties: parent and rank (or height). There are two possible approaches: objects in set would need to implement some specific interface (T: IDisjointSetExtraInfo) or we could maintain some internal dictionary Dictionary<T, ExtraInfo> and store required extra information this way. As usual there are pros and cons of both approaches.

Trade-offs everywhere

The approach with dictionary is more generic, so I’m going to use it, and allow any T, with no constraints (apart from equality).

I’ve originally needed an implementation in Kotlin but as solution is quite generic I’ve also added an implementation in F# to my ever growing library-of-data-structures-which-I-may-want-to-use-in-F#-on-day (TM).

Tag

Let’s start with encapsulation of, mentioned before, “extra info”:

1
2
3
4
5
// Kotlin
private class Tag() {
    var parent = this
    var height = 0
}
1
2
3
4
5
// F#
module DisjointSet =
    type private Tag() as this =
        member val parent = this with get, set
        member val height = 0 with get, set

(Completely off-topic: what F# compiler generates here is extremely puzzling, I understand it handles parent = this but it still puzzles me. Check it with ILSpy if you dare)

So, we have extra info class (called Tag), so far.

Find

We can implement find with path compression which is just following parent link on the way up and updating it on the way back:

1
2
3
4
5
6
// Kotlin
private fun find(tag: Tag): Tag {
    if (tag.parent != tag)
        tag.parent = find(tag.parent)
    return tag.parent
}
1
2
3
4
5
// F#
let rec private find (tag: Tag) =
    if tag.parent <> tag then
        tag.parent <- find(tag.parent)
    tag.parent

Merge

Implementing merge (or union) is a little bit complicated, but just a little. We need to find roots of both sets. If they are the same item, it means that objects are already in the same set therefore there is nothing to merge. If roots are different, they are in different sets, so we need to merge them by setting parent property of one root to the other one, potentially updating height (or rank):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// Kotlin
private fun merge(x: Tag, y: Tag) {
    val xroot = find(x)
    val yroot = find(y)

    if (xroot == yroot)
        return

    if (xroot.height < yroot.height) {
        xroot.parent = yroot
    } else {
        yroot.parent = xroot
        if (xroot.height == yroot.height)
            xroot.height++
    }
}
1
2
3
4
5
6
7
8
9
10
// F#
let private merge tagA tagB =
    match find(tagA), find(tagB) with
    | rootA, rootB when rootA <> rootB ->
        match rootA.height - rootB.height with
        | balance when balance >= 0 ->
            rootB.parent <- rootA
            if balance = 0 then rootA.height <- rootA.height + 1
        | _ -> rootA.parent <- rootB
    | _ -> ()

Map

Now, we can implement the translation layer between Tag and T, most likely a class encapsulating a dictionary:

1
2
3
4
5
// Kotlin
class DisjointSet<T> {
    private val map = mutableMapOf<T, Tag>()
    //...
}
1
2
3
4
// F#
type DisjointSet<'T when 'T : equality>() =
    let map = Dictionary<'T, Tag>()
    //...

Test

Find method, implemented before, makes sense only in a domain of tags which are not exposed outside this module/package. The value returned by find is also not really worth keeping as it may change all the time while sets are merged. What we want to expose though is the function which will test if two items are in the same set.

There are two possible optimizations here:

  • We do not need to go though the process if both items (both Ts) are the same item (if (x == y) return true)
  • if one of the items is not in dictionary at all, it means that it was not taking part in any merge operation yet, therefore it cannot be in the same set as the other one
1
2
3
4
5
6
7
// Kotlin
fun test(x: T, y: T): Boolean {
    if (x == y) return true
    val xtag = map[x]
    val ytag = map[y]
    return xtag != null && ytag != null && find(xtag) == find(ytag)
}
1
2
3
4
5
6
7
8
9
10
11
// F#
let get key =
    let result = ref Unchecked.defaultof<Tag>
    match map.TryGetValue(key, result) with | false -> None | _ -> Some result.Value

member x.Test(keyA: 'T, keyB: 'T) =
    (keyA = keyB) || (
        match get keyA, get keyB with
        | Some tagA, Some tagB -> find(tagA) = find(tagB)
        | _ -> false
    )

The get method in F# is a little wrapper for TryGetValue. It wraps quite ugly Key -> 'Value byref -> bool and converts it into much more functional 'Key -> 'Value option.

Merge

We had merge already implemented, all we need is handling the translation between T and Tag:

1
2
3
4
5
6
// Kotlin
fun merge(x: T, y: T) {
    val xtag = map.getOrPut(x) { Tag() }
    val ytag = map.getOrPut(y) { Tag() }
    merge(xtag, ytag)
}
1
2
3
4
5
6
// F#
let set key tag = map.[key] <- tag; tag
let getOrCreate key = match get key with | Some v -> v | None -> Tag() |> set key

member x.Merge(keyA: 'T, keyB: 'T) =
    merge (getOrCreate keyA) (getOrCreate keyB)

And again, we needed a little wrapper functions in F#. Sometimes .NET disappoints me with quite minimalistic API.

Regardless of my complaints, that’s it. Please mention disjoint-set when talking to your friends, maybe when discussing Ackermann function or generating mazes using Kruskal’s algorithm.