Maze generator with Fable

Redgate’s first ever coding challenge

For quite some time I was looking for an excuse to use Fable. Fable is F# to JavaScript compiler. I generally shy away from JavaScript, as I am biased towards backend but as a big fan of F# I wanted to play a little with Fable (and Scala.js actually). On top of that, I wanted to try some other technologies I’ve never used before: VirtualDom (maybe React), Webpack, Pixi.js. All I needed was an excuse…

I’ve found Redgate’s first ever coding challenge on LinkedIn and I decided to do it with Fable in the browser. The challenge is about writing an application to generate mazes (thus the Daedalus reference). I wasn’t going to apply as my solution is probably the most trivial one using “randomized DFS”, so there is nothing to show off, but, I wanted to use those tools.

EDIT: eventually, it did apply

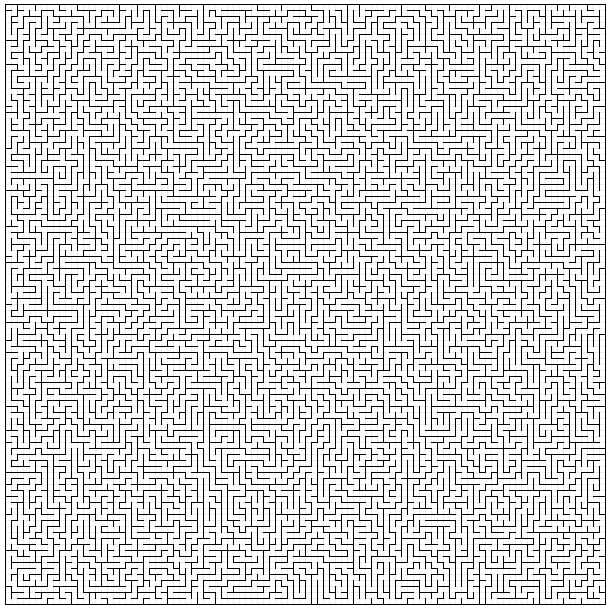
100x100

Initially solution was building SVG with VirtualDOM. It was very neat as Fable/VirtualDOM uses Elm architecture (check Fable samples page). It was fast enough to solve the problem but unfortunatelly, for bigger mazes (>50x50), not fast enough for live animation. Changing multiple <rect> to one long multipart <path> made it a little bit faster (~20%) but it still wasn’t good enough and it was definitely slowing down further it went.

The final version is not as ambitious, uses jQuery and jCanvas. Presentation layer is very old school, but it works and is very fast (relatively speaking, of course). Note, I could deal with the <canvas> without any supporting libraries, but one of my goals was to investigate and evaluate integration with native JavaScript libraries as, in my opinion, integration is one of the most important aspects of any X-to-JavaScript transpiler.

“You’re very clever, young man, very clever,” said the old lady. “But it’s functions all the way down!”

Scott Wlaschin says “No abstraction is too small”. I agree, I’m a big fan of “extracting abstraction” and I’m so glad F# supports and encourages local one-liners. I believe problems should be decomposed into small managable chunks first and then composed back into solution. Things should be named appropriately as well. Let me use example given by Kevlin Henney (it’s actually Dan North’s example but I have no link): 

1
2
3
if (portfolioIdsByTraderId.get(trader.getId()).containsKey(portfolio.getId())) {
    ...
}

Even if we understand every single word in this statement, it is still unclear what purpose it serves. It is not abstract enough, it contains too much of “implementation”. Maybe we should consider this as an alternative:

1
2
3
if (trader.canView(portfolio)) {
    ...
}

Yup, that’s much better.

For every solution, at some point there will be a need for some “ugly implementation details”. It is just nicer when you can push it far away from business logic so it does not get in a way when you try to reason about what this code “actually does”.

In this article I will use a some one-liners. They might seem like overkill for this task but this is primarily fun project and using them is fun!

The algorithm

There are few algorithms listed on Wikipedia and randomized depth-first search is probably the simplest one.

It has two disadvantages:

  • solution has a low branching factor and contain many long corridors (please note, that this issue was addressed in following blogpost)
  • solution does not contain cycles - This problem applies to most of solutions from Wikipedia. It seems that “maze generation problem” is perceived as “random spanning tree”. Cycles can be seen as shortcuts, therefore making it easier to solve for potential maze explorer, but also they open the door to “be lost forever”, making it infinitely harder. Trade-offs, trade-off, trade-offs.

I’m going to decompose the solution into smaller pieces instead of using single monolithic function.

A physicist and a mathematician setting in a faculty lounge. Suddenly, the coffee machine catches on fire. The physicist grabs a bucket and leaps towards the sink, fills the bucket with water and puts out the fire. The second day, the same two sit in the same lounge. Again, the coffee machine catches on fire. This time, the mathematician stands up, gets a bucket, hands the bucket to the physicist, thus reducing the problem to a previously solved one.

Let’s start with generic depth-first search then:

1
2
3
4
5
6
7
8
9
10
module DFS =
    // ('T -> unit) -> ('T -> bool) -> ('T -> 'T seq) -> 'T -> 'T seq
    let rec traverse mark test fanout node =
        seq {
            match node |> test with
            | false ->
                yield node |> apply mark
                yield! node |> fanout |> Seq.collect (traverse mark test fanout)
            | _ -> ()
        }

where mark: 'T -> unit is the function which will take a node and mark it as visited, test: 'T -> bool will test is node has been visisted already, fanout: 'T -> 'T seq will take a node and return a sequence of connected nodes (neighbours?) and finally node: 'T is just a starting point.

The algorithm goes like this:

  • if node has not been visited yet (node |> test) mark it as visisted (apply mark) and return it (yield).
  • for every connected node (node |> fanout), rinse and repeat (Seq.collect traverse mark test fanout)

If you don’t know what apply does I would recommend my other post.

Done. We can go home… OK, I’m just joking.

NOTE: This solution is vulnerable to stack overflow as it goes deeper and deeper with every visited node. The actual solution uses different implementation of DFS which is using while loop and lists to simulate call stack (I called it stackless which is a little self contradicting, isn’t it?). Idea is absolutely the same though, but code is less elegant.

The domain

So, we have an algorithms. Now we need domain model.

Initially, the domain of this problem consisted of the World, which is a collection of Rooms which in turn have their Location and are connected (or not) through Exits. Not all of those concepts are needed for the algorithm. They may or may not be needed by presentation layer but we probably shouldn’t jump ahead, I guess.

So, let’s start with Location (x and y coordinates) and Direction (north, east, etc…):

1
2
type Location = int * int
type Direction = | North | East | South | West

There is also a relation between directions (opposite) and a function allowing to move from one location in given direction (shift).

1
2
3
4
5
6
7
8
9
let opposite direction = // Direction -> Direction
    match direction with
    | North -> South | South -> North
    | West -> East | East -> West

let shift (x, y) direction = // Location -> Direction -> Location
    match direction with
    | North -> (x, y - 1) | South -> (x, y + 1)
    | East -> (x + 1, y) | West -> (x - 1, y)

Traversing a maze is about actions (or moves). Theoretically, we could model it with single type of action (move south from 5,4 to 5,5), but first move (which is start at 0,0) does not have source nor direction and with language like F# you should not compromise on domain model aka make illegal state unrepresentable.
So, I ended up with two possible actions: teleporting to starting location and moving from one location to another:

1
2
3
type Action =
    | InitAt of Location
    | MoveTo of Location * Direction * Location

The Action has it’s “property” called target, the Location where it ends:

1
2
3
4
5
// Action -> Location
let targetOf action = 
    match action with 
    | InitAt location -> location 
    | MoveTo (_, _, location) -> location

Bringing “The algorithm” and “The domain” together

It is important to realize, that DFS in this case does not really traverse rooms (graph nodes), it actually traverses actions (graph edges), although it is the room which is visted (not action).

Long story short, there is some glue needed between “The algorithm” and “The domain” presented above.

Let’s start with some one-liners for solution:

1
2
3
4
5
6
7
8
9
10
11
// int -> int -> Action seq
let buildMaze width height =
    // Location -> bool
    let isValid (x, y) = x >= 0 && y >= 0 && x < width && y < height
    let visited = HashSet()
    let encode (x, y) = y*width + x // Location -> int
    // Location -> unit 
    let mark location = location |> encode |> visited.Add |> ignore
    // Location -> bool
    let test location = location |> encode |> visited.Contains
    //...

NOTE: HashSet in Fable is modelled using JavaScript Set which does not use structural equality (I learnt it the hard way). Therefore two identical tuples would not be recognised as such. We need to encode tuple value as something which is properly handled by Set. Encoding tuple as single int is one options, encoding it as string would be also valid (but a little but slower, I suppose).

We have function to test is given location is valid for given maze size (isValid), we can test if action points to a room which has been visisted before (test) and mark the location as visisted if needed (mark). That is just a small vocabulary for our problem.

It’s time to define fanout method which will return all valid the neighbours: 

1
2
3
4
5
// Location -> Action seq
let fanout source =
    [| West; North; East; South |] 
    |> Array.map (fun direction -> MoveTo (source, direction, shift source direction))
    |> Array.filter (targetOf >> isValid)

As you can see, it takes a source location, then generates a sequence of MoveTo actions in every direction and then eliminates the ones with invalid target locations (the ones which would point outside the maze). You may wonder why fanout returns candidates in pretty deterministic order. And that’s fair question. I just don’t think randomization stategy is responsibility of fanout function, I think we can postpone this decision (at least for 5 more seconds).

We have all building blocks ready now and it’s time to call DFS.traverse (or DFS.stackless). As I said before traverse operate on actions (not locations), and functions we defined so far work on locations. We will need some adapters, and some randomization of fanout output.

Functional composition to the rescue: 

1
2
InitAt (0, 0) 
|> DFS.traverse (targetOf >> mark) (targetOf >> test) (targetOf >> fanout >> Array.shuffle)

It starts with action (InitAt (0, 0)), and uses composition to adapt input argument of mark, test and fanout. It also randomizes the output of fanout with shuffle.

And this sequence of actions it the result of buildMaze.

Done, again. OK, we need presentation.

Presentation

Without getting into much details we need a <button> and a <canvas>:

1
2
<button id="restart" type="button" class="btn">Restart</button>
<canvas id="canvas" class="maze"></canvas>

That’s the UI. Right? Yeah, kind of. Be aware that the code here is for illustration only, please refer to github for actual working sources.

Let’s start with importing native JavaScript libraries: 

1
2
let jq = importDefault<obj> "jquery"
(importDefault<obj> "jcanvas") $ (jq, Browser.window) |> ignore

As you can see there a little bit weird syntax when accessing arbitrary JavaScript objects. The good news is you can import TypeScript .d.ts definition files into Fable to have strongly typed interfaces. In this case though, I used so little of it, that I could manage dynamic invocation.

Long story short, importDefault get’s translated into require (for CommonJS). The $ operator is invoke, ? operator is get and <- is set. $ operator in many cases can be ommited.
So, a ? b ? c(77) would be translated to a.b.c(77); while a ? b ? c <- 11 would be translated to a.b.c = 11;.

Please note, that as there is an assumptions that everything returns obj (or obj -> obj which is also an obj). F# does not like dangling result values so you need to ignore results you don’t care about. I definitely recommend referring to Fable website for more details.

Let’s define some constants:

1
2
3
4
5
6
7
let [<Literal>] WORLD_WIDTH = 100
let [<Literal>] WORLD_HEIGHT = 100
let [<Literal>] ROOM_SIZE = 5
let [<Literal>] DOOR_SIZE = 1

let [<Literal>] ROOM_COLOR = "#fff"
let [<Literal>] DOOR_COLOR = "#eee"

and a simple function to convert world location to coordinates in pixels:

1
2
let toPixel (x, y) = // Location -> (int * int) // and yes, I'm cheting with types a little
    x*ROOM_SIZE + (x + 1)*DOOR_SIZE, y*ROOM_SIZE + (y + 1)*DOOR_SIZE

Let’s set the <canvas> up, by setting width, height, viewbox and viewport (using jQuery):

1
2
3
4
5
6
7
let w, h = toPixel (WORLD_WIDTH, WORLD_HEIGHT)
let canvas = jq $ ("#canvas")
canvas 
    ? attr("width", w) ? attr("height", h) 
    ? attr("viewbox", sprintf "0 0 %d %d" w h) 
    ? attr("viewport", sprintf "0 0 %d %d" w h) 
    |> ignore

and wire click event on “Restart” button:

1
2
3
4
5
6
7
let mutable cancel = id
let button = jq $ ("#restart")  
button ? click(fun _ ->
    cancel ()
    canvas ? clearCanvas () |> ignore
    cancel <- startAnimation canvas
) |> ignore

The thing with cancel might be a little bit unclear. Function startAnimation will return a function (function returning function, yes) which can be called to cancel animation. So next time Restart button is pressed previous animation will be cancelled before starting new one. To avoid null (or None) checking (on first run) cancel just gets initialized with function which does nothing (yes, id is a function which does nothing).

Back to solution, when button is pressed potential old animation is cancelled (cancel()), canvas is cleared (canvas ? clearCanvas () |> ignore) and new animation is started (cancel <- startAnimation canvas).

There is only one method left, then:

1
let startAnimation canvas = // ...

Please note, the code below in the scope of startAnimation.

We will definitely need to draw rectangles on canvas, and that’s kind of all we are going to do. I will use jCanvas to do this, but it is an overkill, of course, it could (and should?) be done with browser API, but I’m exploring here, right?
As with dynamic invocation eveything is obj we want to add some types when JavaScript and Fable meets. Let’s wrap jCanvas.drawRect first into drawBox function:

1
2
3
4
5
6
7
8
let drawBox (color: string) (x: int) (y: int) (w: int) (h: int) =
    let rect = 
        createObj [ 
            "fillStyle" ==> color
            "x" ==> x; "y" ==> y; "width" ==> w; "height" ==> h 
            "fromCenter" ==> false 
        ]
    canvas ? drawRect(rect) |> ignore

Yup. Done. Not pretty but done. We can forget about this traumatic experience now. It actually generates quite readable code:

1
2
3
4
5
6
7
8
9
var rect = {
    fillStyle: color,
    x: x,
    y: y,
    width: w,
    height: h,
    fromCenter: false
};
canvas.drawRect(rect);

From now on, we can forget about JavaScript interop again. We can just use drawBox and implement drawRoom to draw a room, and drawDoor to draw a door: 

1
2
3
4
5
6
7
8
9
10
11
12
// Location -> unit
let drawRoom location =
    let x, y = toPixel location in drawBox ROOM_COLOR x y ROOM_SIZE ROOM_SIZE

// Location -> Direction -> unit    
let drawDoor location direction =
    let x, y = toPixel location
    match direction with
    | North -> drawBox DOOR_COLOR x (y - DOOR_SIZE) ROOM_SIZE DOOR_SIZE
    | South -> drawBox DOOR_COLOR x (y + ROOM_SIZE) ROOM_SIZE DOOR_SIZE
    | East -> drawBox DOOR_COLOR (x + ROOM_SIZE) y DOOR_SIZE ROOM_SIZE
    | West -> drawBox DOOR_COLOR (x - DOOR_SIZE) y DOOR_SIZE ROOM_SIZE

Room is drawn as big square, while Door is just a slim rectangle (depends on relation between DOOR_SIZE and ROOM_SIZE). As you can see doors have different shape depending on direction (for example: North vs East).

5x5

Now, we need to start traversing the maze:

1
let mutable action = buildMaze WORLD_WIDTH WORLD_HEIGHT |> Enumerator.create

You can notice Enumerator here, which might be a little bit cryptic but it just provides slighlty more F#-ish way to use IEnumerable<T> interface.

The last part is the animation loop, we need to draw actions as they come. Let’s schedule a callback every 1/60th of a second (should I use requestAnimationFrame here?) which will take current frame (well… action), draw adequate objects (drawRoom and drawDoor) and then proceed to next action (action <- action |> Option.bind Enumerator.next):

1
2
3
4
5
6
7
8
9
10
11
12
let mutable cancel = id
cancel <- Time.interval (1.0 / 60.0) (fun _ ->
    match action |> Option.map Enumerator.value with
    | None -> cancel ()
    | Some (InitAt location) -> 
        drawRoom location
    | Some (MoveTo (_, direction, location)) -> 
        drawRoom location
        drawDoor location (opposite direction)
    action <- action |> Option.bind Enumerator.next 
)
cancel

The last line returns cancel (returns a function, but does not call it) from startAnimation so animation can be externally cancelled.
Note: Time.interval is just a wrapper for setInterval and clearInterval to have more F#-ish experience:

1
2
3
4
5
6
module Time =
    open Fable.Import.Browser
    // float -> (unit -> unit) -> (unit -> unit)
    let interval seconds (action: unit -> unit) =
        let disposable = window.setInterval (action, seconds * 1000.0)
        fun () -> window.clearInterval(disposable)

I guess that’s it.

You can find solution on github. It actually has many branches as I was trying many approaches. I started with “Immutable domain with VirtualDOM to generate SVG”, then I switched to “Mutable domain with VirtualDOM to generate SVG paths”, then I switched to “Mutable domain with jCanvas” and then I realized that half of domain was actually needed by VirtualDOM approach only. So, last incarnation if Daedalus is “Mutable mini domain with jCanvas”.

If you want to just see it work, you can find it here

Dealing with “low branching factor”

As mentioned DFS has a problem with low branching factor. I’ll try to address the problem in next blogpost.

Thanks