Kruskal/DFS hybrid with reduced branching factor

Read original blog-post first

This is just an update to previous blog-post titled Kruskal, Kotlin, and Hex Tiles. I assume you read it, otherwise some things may not make sense.

Problem with “pure” algorithms

We already tried Depth-First Search and Kruskal’s algorithm. They both have some disadvantages. Depth-First Search has low branching factor, meaning that is does not branch unless it gets stuck, so it actually can create one very long path through the whole maze to the point where it is hard to call it “maze” anymore.
On the other side there is Kruskal’s algorithms which is all about branching. The problem with branching is that even if it creates a dead-end the length of dead-end branch is quite often low (let’s say one or two “rooms”) and is very easy to spot.
The “challenge” was to create algorithm which is a hybrid of Depth-First Search and Kruskal’s algorithm.

Original Kruskal's algorithm. Branches, branches everywhere

A Trailblazer algorithm

For this I needed a DFS algorithm using the same domain model as previously implemented Kruskal’s algorithm. It assumed existence of nodes and edges, having no constraint on node (vertex) and expecting edge to be a pair of nodes (vertices):

1
2
3
4
interface Edge<N> {
    val A: N
    val B: N
}

Algorithm itself had very simple interface, it was taking a sequence of edges (most likely randomized), and provided a method called next() returning next edge forming spanning tree. Please note that in languages with generators (Kotlin is not blessed with them, yet) it could be implemented as function taking a sequence of edges (Sequence<E>) and a returning sequence of edges (Sequence<E>). It had to define method next() instead which just returns next edge (equivalent of yield return) or null (kind-of yield break) if no more edges can be found:

1
2
3
4
5
class Kruskal<N, E : Edge<N>>(edges: Sequence<E>) {
    fun next(): E? {
        // implementation
    }
}

This algorithm will have similar interface (although there is no explicitly defined interface) returning sequence of edges:

1
2
3
4
5
class Trailblazer<N, E : Edge<N>>(...) {
    fun next(): E? {
        // implementation
    }
}

I called it Trailblazer because it is not exactly a Depth-First Search as it does not have backtracking. Backtracking in DFS is used to handle dead-ends (by branching), while in this hybrid algorithm branching is handled by Kruskal’s algorithm, so trailblazer is expected to just push forward.

There is a slight impedance between model used by Kruskal’s algorithm and Trailblazer, so the latter will use some helper methods to adapt:

1
2
3
4
5
6
7
class Trailblazer<N, E : Edge<N>>(edges: (N) -> Sequence<E>) {
    private val edges = edges
    private val visited = mutableSetOf<N>()
    private var head: N? = null

    // ...
}

it will need a function (edges) which will provide sequence of edges going out of given node. It will need a set of already visited nodes (visited) and current location (head).

Edges in “Kruskal’s” model are just a pairs of nodes, while for Trailblazer direction is very important. Therefore we will need a method to find “opposite end” of an edge:

1
2
3
4
5
6
private fun opposite(node: N, edge: E): N? =
        when (node) {
            edge.A -> edge.B
            edge.B -> edge.A
            else -> null
        }

we will also need mark visited nodes and optionally move head to newly visited one. This method will also return true if node has been just added (meaning has not been visited before):

1
2
3
4
5
fun visit(node: N, reset: Boolean = false): Boolean {
    val added = visited.add(node)
    if (reset && added) head = node
    return added
}

This does not look pretty, I have to admit, but it helped keep next method quite short:

1
2
3
4
fun next(): E? {
    val current = head ?: return null
    return edges(current).firstOrNull { visit(opposite(current, it)!!, true) }
}

I actually like val current = head ?: return null syntax. Kotlin allow you to put control statements like return, break and continue in places where you would expect expressions, when it makes expression value irrelevant. In this case it will extract value from nullable head and put it into current, or it will exit this method returning null immediately. It’s kind-of “something or die()” in PHP.
After that, it takes all edges going out of current node and finds first which opposite end has not been visited yet. So it is exactly like DFS, it just does not have backtracking.

Bind two algorithms together

These two (Kruskal and Trailblazer) algorithms will have to work together, and they need to expose some methods for communication.
First, Kruskal, needs to expose ability to merge node sets (it is the most important concepts in Kruskal’s algorithm, so if you don’t know what I’m talking about please refer to previous blog-post):

1
2
3
4
class Kruskal<N, E : Edge<N>>(...) {
    // ...
    fun merge(a: N, b: N) = sets.merge(a, b)
}

On the other side of the fence, Trailblazer algorithm will need to be restarted every time Kruskal jumps from one location to another: 

1
2
3
4
class Trailblazer<N, E : Edge<N>>(...) {
    // ...
    fun reset(node: N) { head = node }
}

That’s all we need.

Let’s do the Hybrid algorithm now. It will use the same “interface”, of course:

1
2
3
4
5
6
class Hybrid<N, E : Edge<N>>(edges: Sequence<E>, threshold: Double, rng: () -> Double) {
    private val rng = rng
    private val threshold = threshold

    fun next(): E? = // ...
}

On top of usual stuff (sequence of edges) it will also take random number generator (rng) and a threshold which will control how biased towards Trailblazer (0.0) or Kruskal (1.0) it will be.

It will also need a function returning outgoing edges for Trailblazer. Let’s start with building a dictionary (map) of all edges:

1
2
3
4
5
6
7
8
9
10
11
private val map = mapEdges(edges)

private fun mapEdges(edges: Sequence<E>): Map<N, List<E>> {
    val result = mutableMapOf<N, MutableList<E>>()
    fun link(node: N, edge: E) = result.getOrPut(node, { mutableListOf() }).add(edge)
    for (edge in edges) {
        link(edge.A, edge)
        link(edge.B, edge)
    }
    return result
}

It goes through all edges and for both ends (nodes A and B) adds this edge as outgoing (link). So, the result is a dictionary from nodes to list of edges (Map<N, List<E>>). There might be an important question to ask here, if those lists need to be shuffled again, but I assume that input sequence was already shuffled, so shuffling already shuffled sequence does not increase its randomness. Although, in this case, there is a chance I’m completely wrong.

We can use this dictionary to define function needed by Trailblazer algorithm (see Trailblazer’s constructor):

1
2
private fun getEdges(node: N): Sequence<E> =
        map[node]?.asSequence() ?: emptySequence<E>()

All those question marks are to handle potential misses (and propagate nulls instead of throwing exceptions). So, what this function does is finds a node in dictionary and returns a sequence of edges incidental to this node or, in case node was not in dictionary, it return empty sequence.

Hybrid algorithm encapsulates both algorithms, original Kruskal and Trailblazer algorithms:

1
2
private val kruskal = Kruskal(edges)
private val trailblazer = Trailblazer({ node: N -> getEdges(node) })

it also combines next functions from both:

1
fun next(): E? = nextTrailblazer() ?: nextKruskal()

which means: try Trailblazer first, and if it fails, try Kruskal’s. If both of them failed then that’s it.
First let’s implement about nextTrailblazer: 

1
2
3
4
private fun nextTrailblazer(): E? =
        (if (rng() < threshold) null else trailblazer.next())?.apply {
            kruskal.merge(A, B)
        }

As you can see, it makes a call if it should use Trailblazer algorithm in this step at all. For example, if threshold is set to 0.1 there is a 10% chance on every step that Trailblazer will stop and switch back to Kruskal. Therefore for threshold set to 1.0 it would be working exactly like original Kruskal and Trailblazer’s step would never be executed. For threshold set to 0.0 it would strongly prefer Trailblazer switching to Kruskal only when Trailblazer hit dead-end.
If it decided to use Trailblazer and Trailblazer actually found an edge, both ends of this edge are added to Kruskal’s disjoint-set, making Kruskal’s part of the algorithm aware of this edge being returned.

On the other side, nextKruskal is implemented as follows:

1
2
3
4
5
6
private fun nextKruskal(): E? =
        kruskal.next()?.apply {
            trailblazer.visit(A)
            trailblazer.visit(B)
            trailblazer.reset(if (rng() < 0.5) A else B)
        }

It takes next edge from Kruskal’s algorithm and if it succeeded, adds marks both ends as visited for Trailblazer algorithm and resets Trailblazer’s starting location.

The presentation layer

There is not really too much to do in presentation layer, there are two lines which have been modified. Actually, it’s still one line too much. If Kruskal and Hybrid implemented same interface from the start it would just one line, but adding interface now is a little bit too late - I just want to make it run. Anyway, it there was an interface it would be interface Sequencer<T> { fun next(): T? }.

So, the lines we need to change:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// here: Kruskal -> Hybrid
fun animate(algorithm: Hybrid<Tile, Door>) {
    algorithm.next()?.apply {
        paint(context)
        handle = window.setTimeout({ animate(algorithm) }, 0)
    }
}

val KRUSKAL_BIAS = 0.1 // new constant to control bias

fun launch() {
    // ...and here: Kruskal -> Hybrid
    animate(Hybrid(
            buildWorld(WORLD_WIDTH, WORLD_HEIGHT).shuffled(), 
            KRUSKAL_BIAS, { Math.random() }))
}

Effect

It seems that it does exactly what I intended. That’s how it looks after few steps:

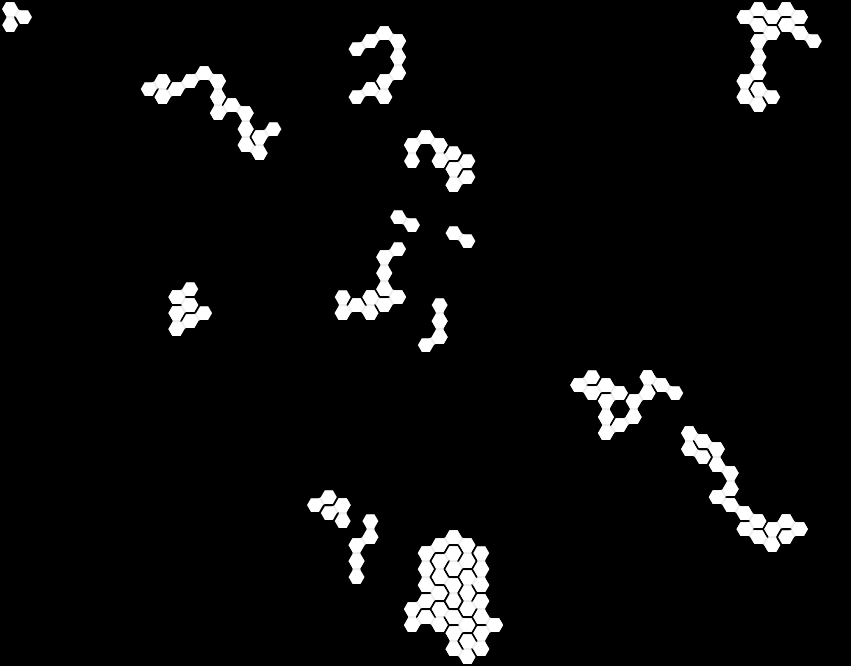
Hybrid algorithm generates longer isolated paths

Conclusion

I really liked OCP in action. I mean, it did require one line to be added to Kruskal’s algorithm to make it work, but arguably merge method should be exposed from the beginning or disjoint-set (sets) should be injected into it. Anyway, Kruskal class has been completely reused, and new algorithm (Hybrid) composes Kruskal and pseudo-DFS (Trailblazer) quite nicely. I could polish it a little bit, but I think it is good-enough.

Sources

You can find sources here or you can just use online demo